Spike trains are considered to be points in an abstract topological space. A spike train metric is a rule which assigns a non-negative number D(Sa,Sb) to pairs of spike trains Sa and Sb which expresses how dissimilar they are.
A metric D is essentially an abstract distance. By definition, metrics have the following properties:
Cost-based metrics fulfill the above general definition of a metric, and are constructed with the following ingredients:
This is a cost-based metric in which the elementary steps and associated costs are:
This is a family of cost-based metrics, parametrized by a "cost per unit time" q (units of 1/sec). The elementary steps and associated costs are:
If q is very small, this becomes the spike count distance. If q is very large, all spike trains are far apart from each other, unless they are nearly identical. For intermediate values of q, the distance between two spike trains is small if they have a similar number of spikes, occurring at similar times.
The motivation for this construction is that neurons which act like coincidence detectors should care about this metric. The value of q corresponds to the temporal precision 1/q of the coincidence detector.
This distance can be calculated efficiently by a dynamic programming algorithm.
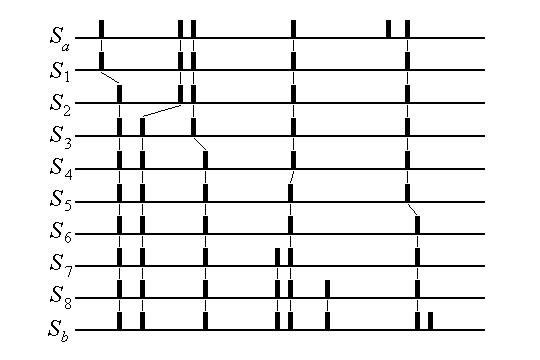
This is a family of cost-based metrics, parametrized by a "cost per unit time" q (units of 1/sec). The elementary steps and associated costs are:
Neurons which show post-tetanic potentiation
and similar mechanisms might care
about this distance. The optimal value of q corresponds to
the temporal precision 1/q of the discrimination between
bursts of different carrier frequencies (or interspike intervals).
top
introduction
cost-based metrics
Dcount
Dspike[q]
Dinterval[q]
generalizations and related
dynamic programming algorithm and links to code
applications and references
Our algorithm can be applied to these generalizations and extensions of the metrics:
Spike time metrics (one kind of cost-based metrics) are a continuous version of edit-length distances, also known as Levenshtein distances. Spike time metrics reduce to the "earth mover distance" (used in image processing and classification) when the number of spikes is identical, and the cost to move a spike is small.
Euclidean distances that are closely related to the spike time metric but are much easier to compute have been introduced by van Rossum (2001). Houghton and Sen (2007) have generalized the von Rossum distance to the multineuronal context. See
van Rossum, M.C.W. (2001) A novel spike distance. Neural Computation 13, 751-763
(download) and
Houghton, C., and Sen, K. (2007) A new multi-neuron spike-train metric.
Neural Computation, in press.
(download).
top
introduction
cost-based metrics
Dcount
Dspike[q]
Dinterval[q]
generalizations and related
dynamic programming algorithm and links to code
applications and references
Hint: it is doubly recursive, and reduces the calculation of the distance between spike trains of length Na and Nb to consideration of spike trains of lengths Na-1 and Nb-1. Think about the constraints on the "world lines" of each spike in the above diagram for Dspike.
Spike Train Analysis Toolkit, a user-friendly implementation from the Laboratory of Neuroinformatics that includes algorithms for information estimation via the direct method, the binless method, and the metric space method.
Fortran, matlab, and c code for the metrics
L. Allisons code for edit-length distances
Flynn O'Connell's python code for spike time distance and a sliding variant
top introduction cost-based metrics Dcount Dspike[q] Dinterval[q] generalizations and related applications and references
Victor, J.D. (2015)
Spike train distance.
In: Encyclopedia of Computational Neuroscience. Ed: D. Jaeger & R. Jung, pp 2808-2814.
Springer New York, Heidelberg ,Dordrecht, London, online.
Summary and download
Houghton, C., and Victor, J.D. (2011) Measuring representational distances – the spike metric approach.
In Understanding Visual Population Codes – Towards a Common Multivariate Framework for Cell Recording and Functional Imaging.
Eds: Nikolaus Kriegeskorte and Gabriel Kreiman. MIT Press, in press.
Abstract and download
Victor, J.D., and Purpura, K.P. (2010) Spike Metrics.
In: Analysis of Parallel Spike Trains. Ed. Stefan Rotter and Sonja Gruen. Springer, pp. 129-156.
Abstract and download
Goldberg, D.H., Victor, J.D., Gardner, E.P., and Gardner, D., (2009) Spike Train Analysis Toolkit:
Enabling wider application of information-theoretic techniques to neurophysiology. Neuroinformatics 7, 165-178.
Abstract, download, and links to code
Victor, J.D. (2005) Spike train metrics. Current Opinion in Neurobiology 15, 585–592.
Abstract and download
Guidolin, A., Desroches, M., Victor, J.D., Purpura, K.P., and Rodrigues, R. (2022)
Geometry of spiking patterns in early visual cortex: a topological data analytic approach.
Journal of the Royal Society Interface, accepted.
Abstract and download
Diez, D.M., Schoenberg, F.P., and Woody, C.D. (2012)
Algorithms for computing spike time distance and point process prototypes with application to feline neuronal responses to acoustic stimuli. J. Neurosci. Meth. 203, 186-192
Download
This describes an alternative algorithm for the multineuronal metric, more efficient than the Aronov (2009) algorithm when there are 5 or more neurons
Dubbs, A.J., Seiler, B.A., and Magnasco, M.O. (2009)
A fast Lp spike alignment metric.
arXiv:0907.3137v2.
Dubbs, A.J., Seiler, B.A., and Magnasco, M.O. (2010)
A fast Lp spike alignment metric.
Neural Computation 11, 2785-2808.
Download
These describe an alternative algorithm based on bipartitre graphs for calculating Dspike and related metrics, and also discuss some theoretical advantages for the use of an L2 metric, rather than the L1 metric described here.
Kreuz, T., Haas, J.S., Morelli, A., Abarbanel, H.D.I., and Politi, A. (2007)
Measuring spike train synchrony.
J Neurosci Methods 165, 151.
Download and
code
This describes another interval-based metric for comparing spike trains, and compares six different metrics, including Dspike
Victor, J.D., Goldberg, D., and Gardner, D. (2007)
Dynamic programming algorithms for comparing multineuronal
spike trains via cost-based metrics and alignments.
J. Neurosci. Meth. 161, 351-360.
Abstract and download
This describes dynamic programming algorithms for computing generalizations of Dspike, parallel in
one or more cost parameters. The algorithm also extends to Lp-metrics
Aronov, D. (2005)
A metric-space approach to the study of information coding by neuronal populations.
Senior Thesis, Columbia University.
Download
Aronov, D., and Victor, J. (2004)
Non-Euclidean properties of spike train metric spaces.
Phys. Rev. E69, 61905.
Abstract, download, and related notes
Aronov, D. (2003)
Fast algorithm for the metric-space analysis of simultaneous responses of multiple single neurons.
J. Neuroscience Methods 124, 175-179.
Abstract, download, and code
Keat, Reinagel, Reid, and Meister (2001) Predicting every spike: a model for the responses of visual neurons. Neuron 30, 803-817.
pdf from Neuron
This describes a generalization to sequences of burst events. The authors also describe a novel approach to pruning the dynamic programming algorithm.
Hitt, Dodge, and Barlow (2003) Information content in responses of Limulus optic nerve fibers. Arvo Abstract 3253. Link to ARVO abstracts
Machens, C.K., Schutze, H., Franz, A., Kolesnikova, O., Stemmler, M.B., Ronacher, B., and Herz, A.V.M. (2001) Single auditory neurons rapidly discriminate conspecific communication signals. Nature Neurosci. 6, 341-342. pdf from Nature Neuroscience pdf from Ronacher's site
Wohlgemuth, S., and Ronacher, B. (2007) Auditory discrimination of amplitude modulations based on metric distances of spike trains. J. Neurophysiol. 97, 3082-3092. pdf from J. Neurophysiol.
Bäcker, A., MacLeod, K., Wehr, M., and Laurent, G. (1998) Disruption of neuronal synchronization impairs reliable reconstruction of odors by beta lobe cells but not by projection neurons of the antennal lobe of the locust. Soc. Neurosci. Abstr. 24, 911.
MacLeod, K., Bäcker A., & Laurent, G. (1998) Who reads temporal information contained across synchronized and oscillatory spike trains? Nature 395, 693-698.
Brasselet, R., Johansson, R.S., and Arleo, A. (2011)
Quantifying neurotransmission reliability through metrics-based information analysis.
Neural Computation 23, 852-81·
Download
Weber, A.I., Saal, H.P., Lieber, J.D., Cheng, J.-W., Manfredi, L.R., Dammann, J.F. III, and Bensmaia, S.J. (2013)
Spatial and temporal codes mediate the tactile perception of natural textures.
Proc. Natl. Acad. Sci. USA 110, 17107-17112.
Download
Di Lorenzo, P., Chen, J.-Y., and Victor, J.D. (2009)
Quality time: Representation of a multidimensional sensory domain through temporal coding. J. Neurosci. 29, 9227-9238.
Abstract and download
Di Lorenzo, P.M, and Victor, J.D. (2003)
Taste response variability and temporal coding in the nucleus of the solitary tract of the rat.
J. Neurophysiol. 90, 1418-1431.
Abstract and download
Kreiman, G., Krahe, R., Metzner, W., Koch, C., & Gabbiani, F. (2000) Robustness and variability of neuronal coding by amplitude-sensitive afferents in the weakly electric fish Eigenmannia. J. Neurophysiol. 84, 189-204. Abstract
Huetz, C., Del Negro, C., Lebas, N., Tarroux, P. & Edeline, J.M. (2006) Contribution of spike timing to the information transmitted by HVC neurons. Eur J Neurosci 24, 1091-108. PubMed entry
Le Wang, Narayan, Grana, Shamir, and Sen (2007)
Cortical discrimination of complex natural stimuli: Can single neurons match behavior?
J. Neurosci. 27,582-589
J. Neurosci. online
The authors use Dspike, Dinterval, and the van Rossum metric.
 Comments and questions
Comments and questions