Introduction: Linear autoregressive models
In a linear autoregressive model of order R, a time series yn
is modelled as a linear combination of R earlier values in the time series,
with the addition of a correction term xn:
ynmodel =
xn -
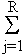 aj yn-j .
aj yn-j .
The autoregressive coefficients aj (j = 1, ... R) are fit by
minimizing the mean-squared difference between the modelled time series
ynmodel and the observed time series
yn. The minimization process results in a system of
linear equations for the coefficients an, known as the
Yule-Walker equations
[Yule, G.U. (1927) On a method of investigating periodicities
in disturbed series with special reference to Wolfer's sunspot numbers.
Phil. Trans. Roy. Soc. Lond. A 226, 267-298].
Conceptually, the time series yn
is considered to be the output of a discrete linear feedback circuit
driven by a noise xn,
in which delay loops of lag j have feedback strength aj.
For Gaussian signals, an autoregressive model often provides
a concise description of the time series yn, and calculation of
the coefficients aj provides an indirect but highly efficient
method of spectral estimation.
top
introduction
nonlinear modelling
NLAR fingerprints
significance testing
references
Nonlinear modelling
In a full nonlinear autoregressive model,
quadratic (or higher-order) terms are added to the linear
autoregressive model. A constant term is also added, to counteract
any net offset due to the quadratic terms:
ynmodel =
xn - a0
- 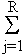 aj yn-j
-
aj yn-j
- 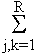 bj,k yn-jyn-k.
bj,k yn-jyn-k.
The autoregressive coefficients aj (j = 0, ... R) and
bj,k (j, k = 1, ...., R)
are fit by
minimizing the mean-squared difference between the modelled time series
ynmodel and the observed time series
yn. The minimization process also results in a system of
linear equations, which are generalizations of the Yule-Walker equations for
the linear autoregressive model.
Conceptually, the time series yn
is considered to be the output of a circuit with nonlinear feedback,
driven by a noise xn. In principle, the coefficients
bj,k describe dynamical features that are not evident in
the power spectrum or related measures.
Although the equations for the
autoregressive coefficients aj and
bj,k are linear, the estimates of these parameters are often
unstable, essentially because a large number of them
must be estimated. This is the motivatation for the
NLAR fingerprint.
introduction
nonlinear modelling
NLAR fingerprints
significance testing
references
NLAR fingerprints
To create the nonlinear autoregressive fingerprint,
only a single term of the full quadratic model is retained,
along with the constant term:
ynmodel =
xn - a0
- 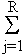 aj yn-j
- bu,v yn-uyn-v.
aj yn-j
- bu,v yn-uyn-v.
The autoregressive coefficients aj (j = 0, ... R) and
the single coefficient bu,v
are fit by
minimizing the mean-squared difference between the modelled time series
ynmodel and the observed time series
yn. This involves estimation of only R+2 parameters
(compared with (R+1)(R+2)/2 equations for the
full quadratic autoregressive model),
and substantially more reliable values for the parameters.
However, like the full quadratic autoregressive model, it provides
a characterization of the nonlinear dynamics of the time series.
The fitting procedure is performed sequentially for all pairs of
lags u and v (u,v = 1, ...., R). The "NLAR fingerprint" consists
(see example)
of a contour map of the residuals
 |ynmodel - yn|2,
parametric in the choice of lags u and v.
|ynmodel - yn|2,
parametric in the choice of lags u and v.
top
introduction
nonlinear modelling
NLAR fingerprints
significance testing
references
Significance testing
Introduction of an additional term into a linear or nonlinear autoregressive
model always improves the fit (in the mean-squared sense).
Akaike [Akaike, H. (1974)
A new look at statistical model identification.
IEEE Trans. Auto. Control AC-19,716-723]
showed that, for a linear autoregressive model,
a significant improvement in the fit is associated
with a reduction in the residual variance of at least 2V/N, where
V is the variance without the candidate additional term, and N is the number
of data points.
We showed that the same criterion, a reduction in residual
variance by at least 2V/N, is a criterion for the significance
of a single nonlinear term as well.
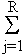 aj yn-j .
aj yn-j .
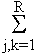 bj,k yn-jyn-k.
bj,k yn-jyn-k.
 |ynmodel - yn|2,
parametric in the choice of lags u and v.
|ynmodel - yn|2,
parametric in the choice of lags u and v.